Appearance of a resonance tells us that there exist a set of parameters for which the response of the system to external signal is “maximal”, at least in some local area in the parameter space. Each resonant frequency of the external signal corresponds to a specific “state” of parameters of the studied system. When the parameters are changing in a random fashion the resonan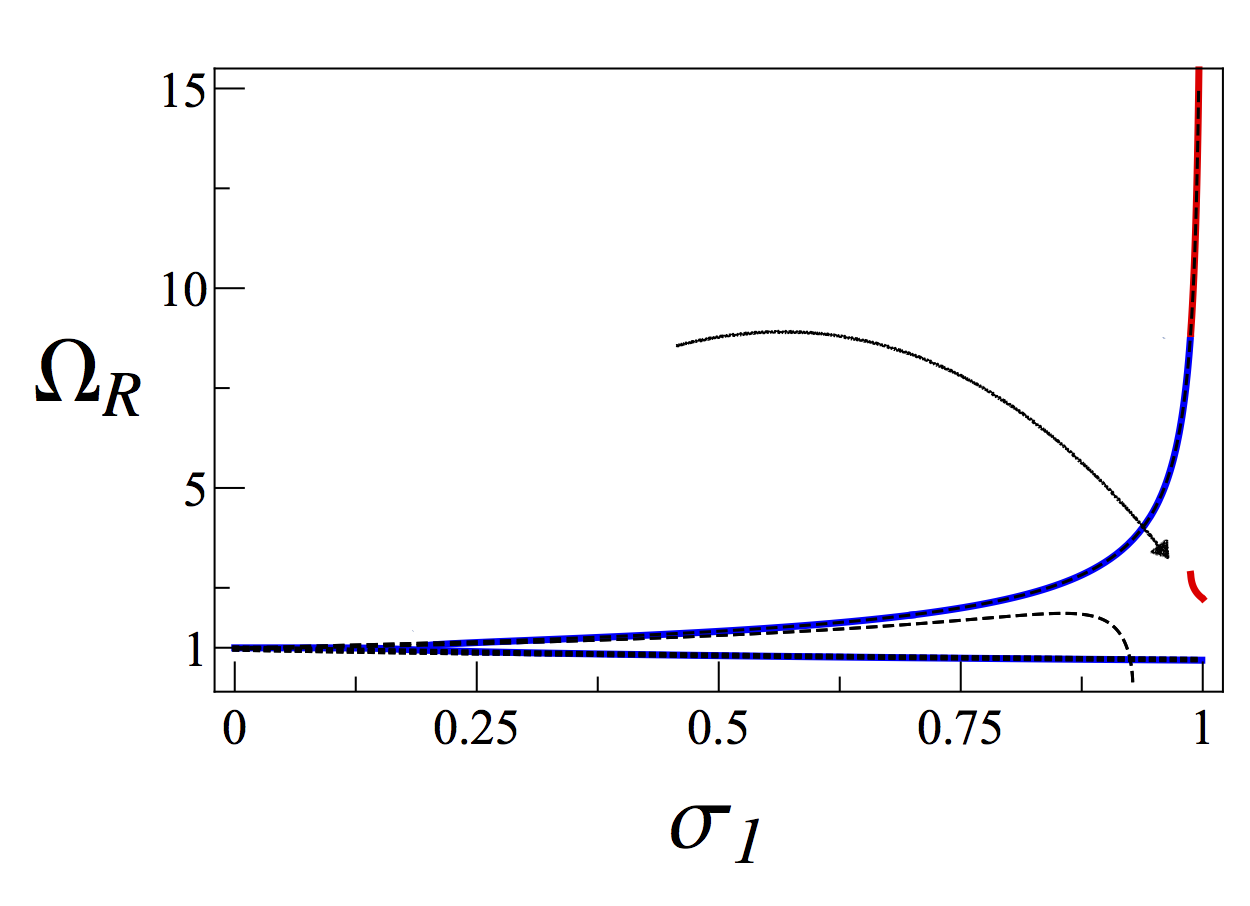
t frequency of the external signal can disappear or transform to some other value. If a specific parameter jumps between several values, for each value there possibly a resonant state (combined with the value of other parameters). One can use appearance of a resonance in order to identify the different states of the randomly changing parameter. It is also true if two parameters are performing those random jumps between different values, a set of values of the two parameters corresponds to a state. This all holds true while for each state a resonance can appear. An interesting feature was observed in our manuscript on multiplicative noises in oscillators. We observed appearance of a resonance for a set of parameters that do not corresponds to a resonance, given this set is not changing as a function of time. This means that for each state state, the system can’t show a resonant behavior. When we allow for transitions between the unfavorable states a resonant behavior arises. This new resonant frequency is shown by the arrow in the figure above. One can maybe claim that the states effectively “entangled” to produce such behavior, but this is a classical system.
